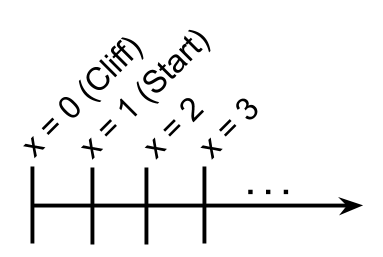
From where he stands, one step toward a cliff would send a drunken man over the edge. He takes random steps, either toward or away from the cliff. At any step, his probability of taking a step away is \(p=\frac{2}{3}\), and his probability of taking a step toward the cliff is \(1-p=\frac{1}{3}\). What is his chance of escaping the cliff?
We begin by representing the cliff as a number line, where \(x=0\) is the edge, \(x=1\) is the man’s starting point, \(x=2\) is \(2\) steps from the edge, and so on:
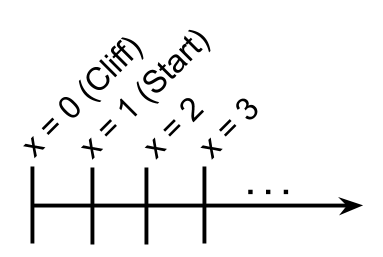
Let \(P_1\) be the probability that the man eventually reaches \(x=0\) (the edge) starting at \(x=1\). We can write \(P_1\) as follows:
\[P_1 = (1-p) + pP_2\]
In the above, \((1-p)\) represents the probability of immediately taking a step towards the edge. The latter part represents the probability of taking a step away and then eventually reaching \(x=0\). Here, as before, \(P_2\) represents the probability that the man eventually reaches \(x=0\) starting at \(x=2\).
We can continue expanding this equation recursively. For example, \(P_2\) can be written as \(P_2 = (1-p)P_1 + pP_3\). However, this does not lead us closer to the solution.
An important insight to observe is that \(P_2 = P_1P_1 = P_1^2\). The first \(P_1\) is equivalent to the probability of moving from \(x=2\) to \(x=1\), and the second \(P_1\) is used in the traditional sense, representing the probability of moving from \(x=1\) to \(x=0\). We can plug this identity into the original equation and apply the quadratic formula to get the following:
\[\begin{split} P_1 &= (1-p) + pP_1^2 \\ &= \frac{1 \pm \sqrt{1 - 4p(1-p)}}{2p} \\ &= \frac{1 \pm (1-2p)}{2p} \\ &= 1, \frac{1-p}{p} \end{split}\]
Applying the solution \(P_1 = \frac{1-p}{p}\) to \(p=\frac{2}{3}\) gives a probability of \(1-P_1 = \frac{1}{2}\) of the man escaping the cliff.