What is the probability that the following quadratic equation has real roots? \[x^2 + 2bx + c =0\]
We begin by applying the quadratic formula to the equation given above:
\[x = \frac{-2b \pm \sqrt{4b^2-4c}}{2}\]
Rearranging the contents of \(\sqrt{4b^2-4c}\) shows that the roots are real if and only if the following holds:
\[4b^2-4c > 0\] \[c < b^2\]

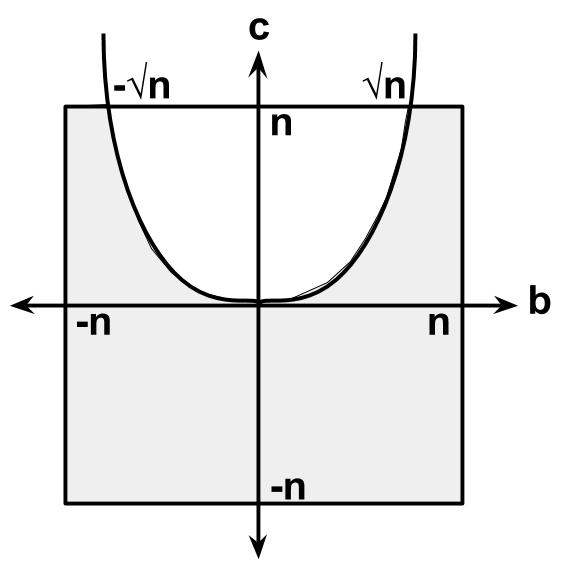
We can calculate the probability that \(c < b^2\) geometrically. We begin by drawing a \(2n\) by \(2n\) square centered at the origin. The graph of \(c=b^2\) intersects the square at \(b=\pm \sqrt{n}\). Within the square, the shaded region below the parabola represents equations with real roots.
To find the probability of real roots, \(P\), we can calculate the proportion of the shaded area with respect to the entire square. We will consider the limiting value of this proportion as \(n\) tends towards \(\infty\):
\[\begin{split} P &= \lim_{n \to \infty} \frac{4n^2 - \int_{-\sqrt{n}}^{\sqrt{n}}n-b^2db}{4n^2} \\ &= \lim_{n \to \infty} \frac{4n^2 - \frac{4}{3}n^{\frac{3}{2}}}{4n^2} \\ &= \lim_{n \to \infty} 1 - \frac{3}{\sqrt{n}} \\ &= 1 \end{split}\]
Thus, the probability of the equation having real roots is \(1\).